约数定理（判断一个数有多少个约数）

判断一个数有多少个约数

介绍

这里有一个蓝桥的真题。
就是判断100！有多少个约数。
原题链接
这就是那个国赛的真题。

那么这里我们就用到了约数定理。

就是任何一个大于一的自然数，如果N不为质数（质数是除了1和它本身，不被任何数整除的数），都可以分解为有限个质数的乘积（指数形式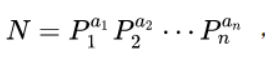）这里的P就是每个质因数，P的指数代表的是含有多少个这样的质因数。如果不会分解质因数的可以看这里

重要的就要来了->约数定理定义

一个大于1的正整数，如果它能被分解为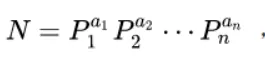

那么它的正因数为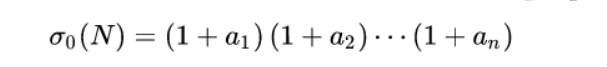就是每个因数数的个数加1然后再逐个相乘。

如果还不会的话我们举个例子

例题：正整数378000共有多少个正约数？
解：将378000分解质因数378000=2^4 × 3 ^3 × 5 ^3 × 7 ^1
由约数个数定理可知378000共有正约数(4+1)×(3+1)×(3+1)×(1+1)=160个。
由于100！太大了，我们可以一个乘数一个乘数来拆分。

源码

这里因为100！太大了，所以我们从1到100遍历，把阶乘拆开，

#include <bits/stdc++.h>

using namespace std;

#define LL long long

#define endl "\n"

const int N = 1e5 + 10;

const int M = 110;

int a[M];

void divide(int x)
{
    for (int i = 2; i <= x / i; i ++ )
    {
        if (x % i == 0)
        {
            int s = 0;
            while(x % i == 0)
            {
                s ++;
                x /= i;
            }
            a[i] += s;
        }
    }
    if (x > 1) a[x] ++;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);

    for (int i = 1; i <= 100; i ++ )
    {
        divide(i);
    }

    LL ans = 1;
    for (int i = 1; i <= 100; i ++ )
    {
        if (a[i])
        {
            ans = ans * (a[i] + 1);
        }
    }

    printf("%lld", ans);
    return 0;
}