二分查找

注意：原数组必须要按照一定的顺序排序，如果没有就先sort一下

二，模板一（常用）

原理

• 每次查找左边的端点。与target比较。

• 如果在这个数组中没有这个数 那么就会返回最接近这个数的数的索引。

记法

q[mid]在target的右边（大于target）就更新右边的端点。
target在哪边就是从哪边开始查，查哪边的端点。这一个target在mid左边，所以是从左边开始查。

源码

int bsearch(int l, int r, int target)
{
    while(l < r)
    {
        int mid = l + r >> 1;
        if (target <= q[mid]) r = mid;
        else l = mid + 1;
    }

    if (q[l] != target) return -1;
    else return l;
}

三，模板二（有坑）

原理

• 每次查找右边的端点和target比较。

• 如果在这个数组中没有这个数 那么就会返回最接近这个数的数的索引。

• 注意： 这里的mid的计算，是多加了个1再除的（向上取整）

• 是为了避免只有两个数发生死循环的可能，索引0和1更新一次mid索引还是 l，那么如果更新了左端点---l = mid，那么相当于l=l，那么左端点会一直不动，但是一直更新的左端点，不会更新右端点，进入死循环。

• 死循环例子： q[2] = {5, 7}。target = 7。

记法

判断的时候，mid在左边（小于等于target）那么就更新左端点。

源码

int bsearch(int l, int r, int target)
{
    while(l < r)
    {
        int mid = l + r + 1 >> 1;
        if (target >= q[mid]) l = mid;
        else r = mid - 1;
    }

    if (q[l] != target) return -1;
    else return l;
}

四，应用

1，普通查找数的索引

• 测试链接

  • 力扣704二分查找

就直接用上面两个模板就行了，注意模板二的坑，然后如果数组中没有改数，那么就会返回一个最接近target的数的索引。

2，具有重复元素的（高阶用法）

• 具体的原理待定

• 测试链接

  • AcWing789数的范围

题目大意： 主要就是这个数组按升序排序，但是有重复元素，找到重复元素的第一个数的索引，和最后一个数的索引。

• 

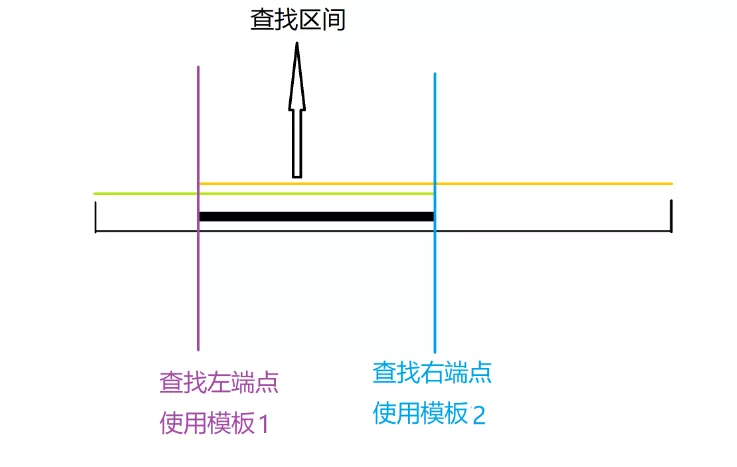
• 找左端点

  • 用模板一就行了，因为模板一 x相当于在mid左边（记法），找左边的x就是左端点，从左端逼近。

• 找右端点

  • 用模板二就行了，因为模板二 x相当于在mid右边，找右边的x就是右端点，从右端逼近。\

五，写法思路

• 首先就是判断从哪个方向开始查，判断target和mid的相对位置。
  • 如果从左边开始查，target就在左边。反之.....
• 根据target的位置想check(mid)函数。
  • 如果target在左边，check(mid)就是target<=q[mid]。反之.....
• 然后再判断mid哪里用不用+1。
  • 如果else里面是r = mid - 1出现了减法就要+1，即int mid = l + r + 1 >> 1。