封闭多边形的面积(笛卡尔坐标系中)

介绍

适用于笛卡尔坐标系，就是普通的x轴、y轴上。

注意，多边形是以最后一个顶点到第一个顶点连接起来封闭的所以要有x[n]=x[0], y[n]=y[0]
而且最后有可能是负数，取个绝对值。
公式如下。

化简后

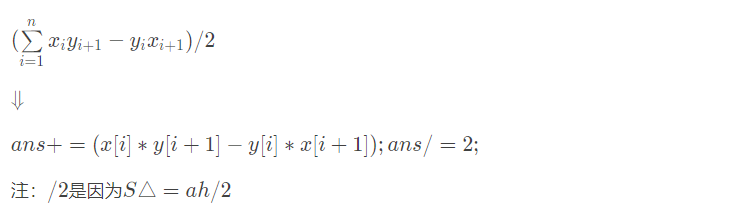
题目

题目描述

给出一个没有缺口的简单多边形，它的边是垂直或者水平的，要求计算多边形的面积。

多边形被放置在一个 $x-y$ 的笛卡尔平面上，它所有的边都平行于两条坐标轴之一。然后按逆时针方向给出各顶点的坐标值。所有的坐标值都是整数，因此多边形的面积也为整数。

输入格式

第一行给出多边形的顶点数 $n$ 。

接下来 $n$ 行，每行给出多边形一个顶点的坐标值 $x$ 和 $y$，用空格隔开。

顶点按逆时针方向逐个给出。多边形最后是靠从最后一个顶点到第一个顶点画一条边来封闭的。

输出格式

一行，一个整数，表示多边形的面积。

样例 #1

样例输入 #1

10
0 0
4 0
4 1
3 1
3 3
2 3
2 2
1 2
1 3
0 3

样例输出 #1

9

提示

对于 $100\%$ 的数据，$1 \le n \le 100$，$-200 \le x,y \le 200$。

代码

void solve()
{
    int n;
    cin >> n;

    for (int i = 0; i < n; i ++ )
    {
        cin >> x[i] >> y[i];
    }

    LL res = 0;
    x[n] = x[0], y[n] = y[0];
    for (int i = 0; i < n; i ++ )
    {
        res += x[i] * y[i + 1] - y[i] * x[i + 1];
    }

    cout << abs(res) / 2 << endl;
}