完全背包问题c++

介绍

完全背包问题的特点就是每个物品有无穷个。

题目链接

朴素版（会TLE)

朴素版讲解

朴素版就是3次遍历

• 不选i个物品
• 选i个物品
  • 选1个物品
  • 选2个物品
  • 等等

朴素版就是遍历体积的时候再加一层遍历，dp[i][j]的j体积下能选几个物品i。

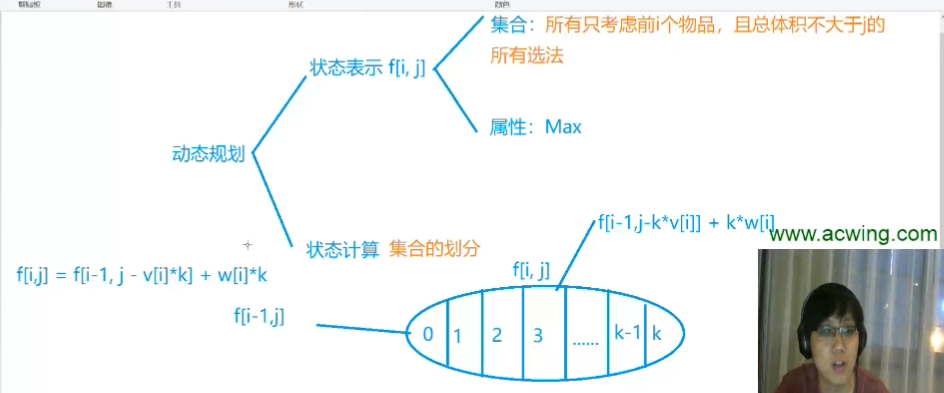
朴素版源码

#include <bits/stdc++.h>

using namespace std;

const int N = 1100;

int n, m;
int v[N], w[N];
int dp[N][N];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++ )
    {
        for (int j = 0; j <= m; j ++ )
        {
            for (int k = 0; k * v[i] <= j; k ++ )
            {
                dp[i][j] = max(dp[i][j], dp[i - 1][j - k * v[i]] + k * w[i]);
            }
        }
    }

    cout << dp[n][m] << endl;

    return 0;
}

优化版

优化版讲解

其实优化版就是将上面那个式子替换了一下，那个f[i, j-v]的式子和那个橙色框内的式子就差个w，所以能替换掉它，这样就不用循环k个了。
那个橙色框内代表的就是选一个物品i、选两个物品i、选三个物品i...。
要怎么理解f[i][j-v]这个式子呢？其实就是将j-v看成一个整体就行了，第一个参数看成是不选这个物品，第二个参数看成是选一个这个物品，等等。

优化版代码

#include <bits/stdc++.h>

using namespace std;

const int N = 1100;

int n, m;
int v[N], w[N];
int dp[N][N];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++ )
    {
        for (int j = 0; j <= m; j ++ )
        {
            // 第二个参数包含了选0个第i物品的情况
            dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i]);
            if (j < v[i]) dp[i][j] = dp[i - 1][j];
        }
    }

    cout << dp[n][m] << endl;

    return 0;
}